Matrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.
Contents |
Example
In numerical analysis, different decompositions are used to implement efficient matrix algorithms.
For instance, when solving a system of linear equations  , the matrix A can be decomposed via the LU decomposition. The LU decomposition factorizes a matrix into a lower triangular matrix L and an upper triangular matrix U. The systems
, the matrix A can be decomposed via the LU decomposition. The LU decomposition factorizes a matrix into a lower triangular matrix L and an upper triangular matrix U. The systems 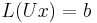 and
and 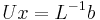 require fewer additions and multiplications to solve, compared with the original system
require fewer additions and multiplications to solve, compared with the original system  , though one might require significantly more digits in inexact arithmetic such as floating point.
, though one might require significantly more digits in inexact arithmetic such as floating point.
Similarly, the QR decomposition expresses A as QR with Q a unitary matrix and R an upper triangular matrix. The system Q(Rx) = b is solved by Rx = QTb = c, and the system Rx = c is solved by 'back substitution'. The number of additions and multiplications required is about twice that of using the LU solver, but no more digits are required in inexact arithmetic because the QR decomposition is numerically stable.
LU decomposition
- Applicable to: square matrix A
- Decomposition:
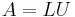 , where L is lower triangular and U is upper triangular
, where L is lower triangular and U is upper triangular - Related: the LDU decomposition is
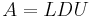 , where L is lower triangular with ones on the diagonal, U is upper triangular with ones on the diagonal, and D is a diagonal matrix.
, where L is lower triangular with ones on the diagonal, U is upper triangular with ones on the diagonal, and D is a diagonal matrix. - Related: the LUP decomposition is
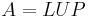 , where L is lower triangular, U is upper triangular, and P is a permutation matrix.
, where L is lower triangular, U is upper triangular, and P is a permutation matrix. - Existence: An LUP decomposition exists for any square matrix A. When P is an identity matrix, the LUP decomposition reduces to the LU decomposition. If the LU decomposition exists, the LDU decomposition does too.[1]
- Comments: The LUP and LU decompositions are useful in solving an n-by-n system of linear equations
 . These decompositions summarize the process of Gaussian elimination in matrix form. Matrix P represents any row interchanges carried out in the process of Gaussian elimination. If Gaussian elimination produces the row echelon form without requiring any row interchanges, then P=I, so an LU decomposition exists.
. These decompositions summarize the process of Gaussian elimination in matrix form. Matrix P represents any row interchanges carried out in the process of Gaussian elimination. If Gaussian elimination produces the row echelon form without requiring any row interchanges, then P=I, so an LU decomposition exists.
LU reduction
Block LU decomposition
Rank factorization
Cholesky decomposition
- Applicable to: square, symmetric, positive definite matrix A
- Decomposition:
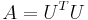 , where U is upper triangular with positive diagonal entries
, where U is upper triangular with positive diagonal entries - Comment: the Cholesky decomposition is a special case of the symmetric LU decomposition, with
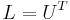 .
. - Comment: the Cholesky decomposition is unique
- Comment: the Cholesky decomposition is also applicable for complex hermitian positive definite matrices
- Comment: An alternative is the LDL decomposition which can avoid extracting square roots.
QR decomposition
- Applicable to: m-by-n matrix A
- Decomposition:
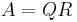 where Q is an orthogonal matrix of size m-by-m, and R is an upper triangular matrix of size m-by-n
where Q is an orthogonal matrix of size m-by-m, and R is an upper triangular matrix of size m-by-n - Comment: The QR decomposition provides an alternative way of solving the system of equations
 without inverting the matrix A. The fact that Q is orthogonal means that
without inverting the matrix A. The fact that Q is orthogonal means that 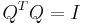 , so that
, so that  is equivalent to
is equivalent to 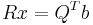 , which is easier to solve since R is triangular.
, which is easier to solve since R is triangular.
RRQR factorization
Singular value decomposition
- Applicable to: m-by-n matrix A.
- Decomposition:
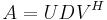 , where D is a nonnegative diagonal matrix, and U and V are unitary matrices, and
, where D is a nonnegative diagonal matrix, and U and V are unitary matrices, and 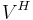 denotes the conjugate transpose of V (or simply the transpose, if V contains real numbers only).
denotes the conjugate transpose of V (or simply the transpose, if V contains real numbers only). - Comment: The diagonal elements of D are called the singular values of A.
- Comment: like the eigendecomposition below, the singular value decomposition involves finding basis directions along which matrix multiplication is equivalent to scalar multiplication, but it has greater generality since the matrix under consideration need not be square.
Eigendecomposition
- Also called spectral decomposition
- Applicable to: square matrix A.
- Decomposition:
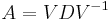 , where D is a diagonal matrix formed from the eigenvalues of A, and the columns of V are the corresponding eigenvectors of A.
, where D is a diagonal matrix formed from the eigenvalues of A, and the columns of V are the corresponding eigenvectors of A. - Existence: An n-by-n matrix A always has n eigenvalues, which can be ordered (in more than one way) to form an n-by-n diagonal matrix D and a corresponding matrix of nonzero columns V that satisfies the eigenvalue equation
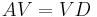 . If the n eigenvalues are distinct (that is, none is equal to any of the others), then V is invertible, implying the decomposition
. If the n eigenvalues are distinct (that is, none is equal to any of the others), then V is invertible, implying the decomposition 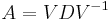 .
. - Comment: The condition of having n distinct eigenvalues is sufficient but not necessary. The necessary and sufficient condition is for each eigenvalue to have geometric multiplicity equal to its algebraic multiplicity.
- Comment: The eigendecomposition is useful for understanding the solution of a system of linear ordinary differential equations or linear difference equations. For example, the difference equation
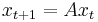 starting from the initial condition
starting from the initial condition 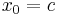 is solved by
is solved by 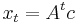 , which is equivalent to
, which is equivalent to 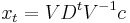 , where V and D are the matrices formed from the eigenvectors and eigenvalues of A. Since D is diagonal, raising it to power
, where V and D are the matrices formed from the eigenvectors and eigenvalues of A. Since D is diagonal, raising it to power 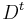 , just involves raising each element on the diagonal to the power t. This is much easier to do and to understand than raising A to power t, since A is usually not diagonal.
, just involves raising each element on the diagonal to the power t. This is much easier to do and to understand than raising A to power t, since A is usually not diagonal.
Jordan decomposition
The Jordan normal form and the Jordan–Chevalley decomposition
- Applicable to: square matrix A
- Comment: the Jordan normal form generalizes the eigendecomposition to cases where there are repeated eigenvalues and cannot be diagonalized, the Jordan–Chevalley decomposition does this without choosing a basis.
Schur decomposition
- Applicable to: square matrix A
- Comment: there are two versions of this decomposition: the complex Schur decomposition and the real Schur decomposition. A complex matrix always has a complex Schur decomposition. A real matrix admits a real Schur decomposition if and only if all of its eigenvalues are real.
- Decomposition (complex version):
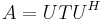 , where U is a unitary matrix,
, where U is a unitary matrix, 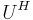 is the conjugate transpose of U, and T is an upper triangular matrix called the complex Schur form which has the eigenvalues of A along its diagonal.
is the conjugate transpose of U, and T is an upper triangular matrix called the complex Schur form which has the eigenvalues of A along its diagonal. - Decomposition (real version):
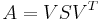 , where A, V, S and
, where A, V, S and 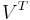 are matrices that contain real numbers only. In this case, V is an orthogonal matrix,
are matrices that contain real numbers only. In this case, V is an orthogonal matrix, 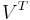 is the transpose of V, and S is a block upper triangular matrix called the real Schur form. The blocks on the diagonal of S are of size 1×1 (in which case they represent real eigenvalues) or 2×2 (in which case they are derived from complex conjugate eigenvalue pairs).
is the transpose of V, and S is a block upper triangular matrix called the real Schur form. The blocks on the diagonal of S are of size 1×1 (in which case they represent real eigenvalues) or 2×2 (in which case they are derived from complex conjugate eigenvalue pairs).
QZ decomposition
- Also called: generalized Schur decomposition
- Applicable to: square matrices A and B
- Comment: there are two versions of this decomposition: complex and real.
- Decomposition (complex version):
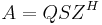 and
and 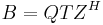 where Q and Z are unitary matrices, the H superscript represents conjugate transpose, and S and T are upper triangular matrices.
where Q and Z are unitary matrices, the H superscript represents conjugate transpose, and S and T are upper triangular matrices. - Comment: in the complex QZ decomposition, the ratios of the diagonal elements of S to the corresponding diagonal elements of T,
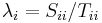 , are the generalized eigenvalues that solve the generalized eigenvalue problem
, are the generalized eigenvalues that solve the generalized eigenvalue problem 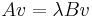 (where
(where  is an unknown scalar and v is an unknown nonzero vector).
is an unknown scalar and v is an unknown nonzero vector). - Decomposition (real version):
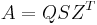 and
and 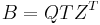 where A, B, Q, Z, S, and T are matrices containing real numbers only. In this case Q and Z are orthogonal matrices, the T superscript represents transposition, and S and T are block upper triangular matrices. The blocks on the diagonal of S and T are of size 1×1 or 2×2.
where A, B, Q, Z, S, and T are matrices containing real numbers only. In this case Q and Z are orthogonal matrices, the T superscript represents transposition, and S and T are block upper triangular matrices. The blocks on the diagonal of S and T are of size 1×1 or 2×2.
Takagi's factorization
- Applicable to: square, complex, symmetric matrix A.
- Decomposition:
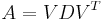 , where D is a real nonnegative diagonal matrix, and V is unitary.
, where D is a real nonnegative diagonal matrix, and V is unitary. 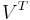 denotes the matrix transpose of V.
denotes the matrix transpose of V. - Comment: the diagonal elements of D are the nonnegative square roots of the eigenvalues of
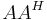 .
. - Comment: V may be complex even if A is real.
Other decompositions
References
- ^ C. Simon and L. Blume (1994), Mathematics for Economists, Ch. 7. Norton, ISBN 0393957330.
External links
- Online Matrix Calculator
- Springer Encyclopaedia of Mathematics » Matrix factorization
- GraphLab GraphLab collaborative filtering library, large scale parallel implementation of matrix decomposition methods (in C++) for multicore.
|
|||||